

Prove Triangle Theorems
Videos and lessons with examples and solutions to help High School students
learn how to prove theorems about triangles.
Related Topics:
Common Core Geometry
Common Core Mathematics
Related Topics:
Common Core Geometry
Common Core Mathematics
Common Core: HSG-SRT.B.4
Theorems include: a line parallel to one side of a triangle divides the other two proportionally, and conversely; the Pythagorean Theorem proved using triangle similarity.
The following figures give the Triangle Proportionality Theorem and the Converse of the Triangle Proportionality Theorem. Scroll down the page for more examples and solutions.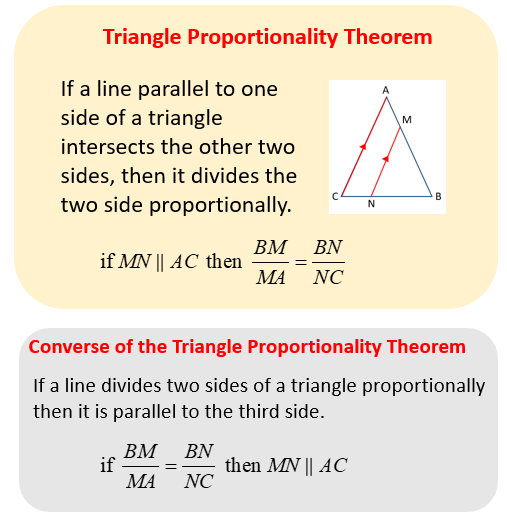
Triangle Proportionality Theorem
The Triangle Proportionality TheoremIf a line parallel to one side of a triangle intersects the other two sides, then it divides those sides proportionally. The segment joining midpoints of two sides of a triangle is parallel to the third side and half the length. Using the Properties of the Triangle Proportionality Theorem to Solve for Unknown Values
Proving -- Converse of the Triangle Proportionality Theorem: If a line divides two sides of a triangle proportionally, then it is parallel to the third side.
Pythagorean Theorem
Prove the Pythagorean Theorem using similar trianglesIn this lesson, you will learn how to prove the Pythagorean Theorem using similar triangles.
Pythagorean Theorem Proof Using Similarity
Proof of the Pythagorean Theorem using similarity. Similar Triangles: Ratio of Areas
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.