Quadratic Formula or Quadratic Equation

What is the Quadratic Formula?
The quadratic formula is a fundamental tool in algebra used to solve quadratic equations. The quadratic formula provides a reliable method for solving any quadratic equation, even those that are difficult or impossible to factor.

A quadratic equation is a polynomial equation of the second degree. It has the general form:
ax² + bx + c = 0
Where ‘a’, ‘b’, and ‘c’ are coefficients, and ‘x’ is the variable. ‘a’ cannot be equal to 0.

The following diagrams gives the Quadratic Formula and how to use it to solve quadratic equations. Scroll down the page for more examples and solutions of the quadratic formula.

The quadratic formula provides the solutions (also called roots) for ‘x’ in a quadratic equation. It is: x = [-b ± √(b² - 4ac)] / 2a

Understanding the Quadratic Formula:
-b ± √(b² - 4ac):
This part indicates that there are typically two solutions: one with a plus sign (+) and one with a minus sign (-).

√(b² - 4ac):
This is the square root of the discriminant (b² - 4ac).
The discriminant determines the nature of the solutions:
If b² - 4ac > 0, there are two distinct real solutions.
If b² - 4ac = 0, there is one real solution (a repeated root).
If b² - 4ac < 0, there are two complex solutions.

• Printable & Online Quadratics & Trinomials Worksheets

  Printable
  Solve Quadratic Equation (use factoring)
  Solve Quadratic Equation (use quadratic formula)
  

  Factoring Trinomials (a = 1)
  Factoring Trinomials (a > 1)
  Factor Perfect Square Trinomials
  

  Factoring Quadratics (a = 1)
  Factoring Quadratics (a > 1)
  Factor Difference of Squares
  Factor Perfect Square Quadratics
  

  Online
  Factor Binomials by Difference of Squares
  Factor Perfect Square Trinomials
  
  Factor Trinomials or Quadratic Equations
  Factor Different Types of Trinomials 1
  Factor Different Types of Trinomials 2
  
  Solve Trinomials using Quadratic Formula
  Find Discriminants of Quadratic Polynomials

Given the quadratic equation ax² + bx + c, we can find the values of x by using the Quadratic Formula:

Let us consider an example.

Example:
Find the values of x for the equation: 4x² + 26x + 12 = 0

Solution:
Step 1: From the equation:

a = 4, b = 26 and c = 12

Step 2: Plug into the formula. The ± sign means there are two values, one with + and the other with –.

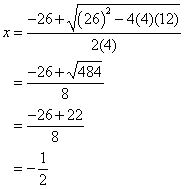
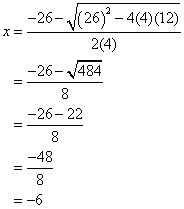
Answer:

Quadratic equations have at most two real solutions, as in the example above.

However, some quadratic equations have only one real solution. If the quadratic equation has only one solution, the expression under the square root symbol in the quadratic formula is equal to 0, and so adding or subtracting 0 yields the same result.

Other quadratic equations have no real solutions; for example, In this case, the expression under the square root symbol is negative, so the entire expression is not a real number.

Have a look at the following videos for more examples on the use of quadratic formula to solve equations:

Using the Quadratic Formula to find solutions to quadratic equations

Example:
Solve 9x² - 9x + 2 = 0

• Show Video Lesson

Example:
Solve 3x² + √11x + 2 = 0

• Show Video Lesson

Example:
Solve 3x² + 5x = 7

• Show Video Lesson

Solving quadratic equations using the quadratic formula.

Examples:
Solve x² - 5x - 6 = 0
Solve 2x² - 4x - 7 = 0

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.