Ratio Word Problems - Two Terms Ratio

Ratio problems are word problems that use ratios to relate the different items in the question.

The main things to be aware about for ratio problems area:

• Change the quantities to the same unit if necessary.
• Write the items in the ratio as a fraction.
• Make sure that you have the same items in the numerator and denominator.

Ratio problems: Two-term Ratios

Example 1:

In a bag of red and green sweets, the ratio of red sweets to green sweets is 3:4. If the bag contains 120 green sweets, how many red sweets are there?

Solution:

Step 1: Assign variables :

Let x = red sweets

Write the items in the ratio as a fraction.

Step 2: Solve the equation

Cross Multiply

3 × 120 = 4 × x
360 = 4x

Isolate variable x

Answer: There are 90 red sweets.

Example 2:

John has 30 marbles, 18 of which are red and 12 of which are blue. Jane has 20 marbles, all of them either red or blue. If the ratio of the red marbles to the blue marbles is the same for both John and Jane, then John has how many more blue marbles than Jane?

Solution:

Step 1: Sentence: Jane has 20 marbles, all of them either red or blue.

Assign variables:

Let x = blue marbles for Jane
20 – x = red marbles for Jane

We get the ratio from John
John has 30 marbles, 18 of which are red and 12 of which are blue.

We use the same ratio for Jane.

Step 2: Solve the equation

Cross Multiply

3 × x = 2 × (20 – x)
3x = 40 – 2x

Isolate variable x

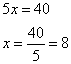
John has 12 blue marbles. So, he has 12 – 8 = 4 more blue marbles than Jane.

Answer: John has 4 more blue marbles than Jane.

Ratios and solving ratio word problems
Examples:
(1) In a class there are 10 males and 15 females. What is the ratio of males to females?
(2) A classroom has a total of 30 students. There are 20 males. What is ratio of males to females?
(3) In a class the ratio of males to females is 4:5. If there are 36 total students, how many females are in the class? How to use proportions to solve ratio word problems?
Examples:
(1) The ratio of salamanders to frogs was 5 to 7. If there were 20 salamanders, how many frogs were there?
(2) If 3 sacks of concrete will make 12 square feet of sidewalk, predict how many sacks of concrete are needed to make 40 square feet of sidewalk.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.