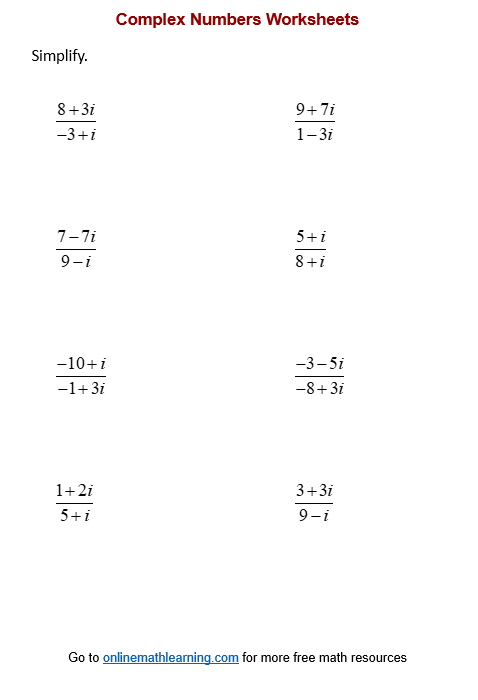Rationalize Complex Number Worksheets

Printable complex numbers worksheets:
Add & Subtract Complex Numbers
Multiply Complex Number
Rationalize Complex Number
Operations with Complex Numbers
Quadratic Equation with Complex Solutions

Examples, solutions, videos, and worksheets to help Algebra II students learn how to rationalize complex numbers or simplifying complex number fractions.

How to rationalize complex numbers?

There are four sets of rationalize complex numbers worksheets

• Rationalize Complex Numbers (Monomial ÷ Monomial)
• Rationalize Complex Numbers (Binomial ÷ Monomial)
• Rationalize Complex Numbers (Monomial ÷ Binomial)
• Rationalize Complex Numbers (Binomial ÷ Binomial)

Rationalizing complex numbers involves removing the imaginary part (usually represented as i) from the denominator of a complex number fraction or expression. This process is commonly used to simplify complex fractions or expressions with imaginary numbers. Here’s how to rationalize a complex number:

1. Identify the Complex Denominator
   Recognize that the denominator of the complex number fraction contains both real and imaginary parts.
2. Multiply by the Conjugate
   Multiply both the numerator and the denominator by the conjugate of the denominator. The conjugate of a complex number in the form a + bi is a − bi.
3. Perform the Multiplication
   Multiply the fraction by the conjugate in both the numerator and the denominator. This step ensures that you are not changing the value of the fraction because you are essentially multiplying it by 1.
4. Simplify
   Simplify the resulting fraction by using distributive properties and combining like terms in both the numerator and the denominator.
5. Check for Further Simplification
   In some cases, you may be able to simplify the expression further by identifying and canceling common factors in the numerator and the denominator.

Example:
Rationalize the complex number fraction (2+3i)/(4−5i)

1. Identify the Complex Denominator.
   The denominator is 4−5i, which contains both real and imaginary parts.
2. Multiply by the Conjugate.
   The conjugate of 4−5i is 4+5i.
3. Perform the Multiplication.
   Multiply both the numerator and the denominator by 4+5i: 4 Simplify.
   Use the distributive property in the numerator and denominator:
   Numerator: (2+3i)(4+5i) = 8 + 10i + 12i - 15 = -7 + 22i
   Denominator: (4-5i)(4+5i) = 16 + 25 = 41

So, (2+3i)/(4−5i) = (-7+22i)/41

Have a look at this video if you need to review how to rationalize complex numbers.

• Divide and Simplify Complex Numbers

Click on the following worksheet to get a printable pdf document.
Scroll down the page for more Rationalize Complex Number Worksheets.

 

More Rationalize Complex Number Worksheets

Printable
(Answers on the second page.)
Rationalize Complex Number Worksheet #1 (Monomial ÷ Monomial)
Rationalize Complex Number Worksheet #2 (Binomial ÷ Monomial)
Rationalize Complex Number Worksheet #3 (Monomial ÷ Binomial)
Rationalize Complex Number Worksheet #4 (Binomial ÷ Binomial)

Online
Powers of i: Positive Exponents
Powers of i: Negative Exponents
Rationalize Complex Number Addition
Rationalize Complex Number Subtraction
Rationalize Complex Number Multiplication
Rationalize Complex Number Division

Rationalize Complex Number: Magnitude (Absolute Value)
Distance Between Two Rationalize Complex Numbers
Midpoint of Two Rationalize Complex Numbers)

Related Lessons & Worksheets

Add & Subtract Complex Number

More Printable Worksheets

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.