Properties of Rhombus
These lessons, with videos, examples and step-by-step solutions, help Geometry students learn about the properties of a rhombus.
Related Pages
Quadrilaterals
Angles In A Quadrilateral
Polygons
More Geometry Lessons
Math Worksheets
The following diagram shows the properties of a rhombus. Scroll down the page for more examples and solutions on using the properties of a rhombus.
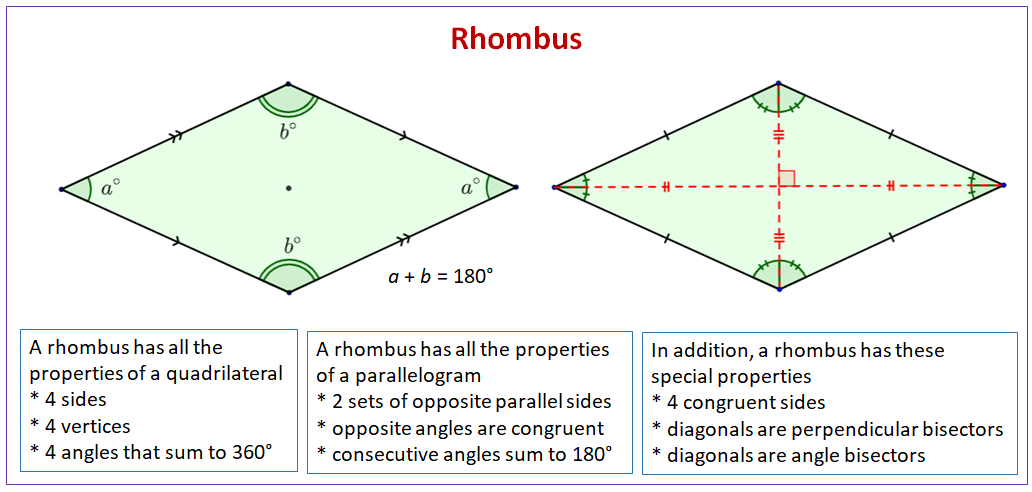
What are the Properties of a Rhombus?
A rhombus is a quadrilateral and has all the properties of a quadrilateral
- 4 sides
- 4 vertices
- 4 angles that sum to 360°
A rhombus is a parallelogram and has all the properties of a parallelogram
- 2 sets of opposite parallel sides
- opposite angles are congruent
- consecutive angles sum to 180°
In addition, a rhombus has these special properties
- 4 congruent sides
- diagonals are perpendicular bisectors
- diagonals are angle bisectors
Apply the properties of a rhombus to solve problems
Rhombus Properties
Properties of rhombi often show up in geometric proofs and many other types of problems.
All parallelogram properties apply to rhombus properties since a rhombus is a type of parallelogram.
In a rhombus, there are
- two pairs of parallel sides,
- four sides that are all congruent to each other,
- diagonals that bisect the angles, and
- diagonals that are perpendicular bisectors of each other.
Properties of a Rhombus
The diagonals of a rhombus are perpendicular and bisect the angles of the rhombus
Area of a Rhombus - Geometry Help
Students learn the formula for the area of a rhombus, and are asked to solve problems using this formula.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.