Sketches Of Some Important Graphs

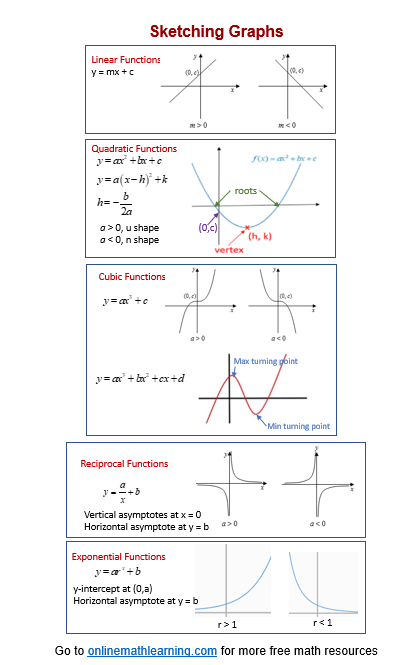
The following are sketches of the graphs of the functions in the form
ax + by = c
y = ax² + bx + c
y = ax³ + b
y = ax³ + bx² + cx
y = a/x + b
y = ar^x + b
where a, b and c are rational numbers and r is a rational, positive number.
Take note of the x-intercept(s), y-intercept(s), turning points, roots, symmetry, vertical and horizontal asymptotes.

 

These are some basic graphs that every algebra student should know.

1. y = mx + b (Linear Function)
2. y = x² (parabola)
3. y = xⁿ
4. y = absolute value of x
5. y = square root of x
6. y =
7. y =
8. y = log_b(x), where b > 1
9. y = a^x

• Show Step-by-step Solutions

This video shows the graphs for the following functions:

1. f(x) = x
2. f(x) = x²
3. f(x) = x³
4. f(x) = square root of x 5*. f*(x) = cube root of x
5. f(x) = absolute value of x

• Show Step-by-step Solutions

How to sketch a cubic graph? (without using calculus)
Sketching the graph of a cubic function involves understanding its key features and using them to plot a representative curve.

1. Determine the End Behavior:
   Look at the Leading Coefficient (a): In the general form f(x) = ax³ + bx² + cx + d:
   If a > 0:
   As x → ∞, f(x) → ∞ (rises to the right)
   As x → -∞, f(x) → -∞ (falls to the left)
   If a < 0:
   As x → ∞, f(x) → -∞ (falls to the right)
   As x → -∞, f(x) → ∞ (rises to the left)
   
2. Find the Intercepts:
   y-intercept:
   Set x = 0 in the function and solve for f(x). This gives you the point (0, f(0)).
   x-intercepts (Roots or Zeros):
   Set f(x) = 0 and solve for x.
   This can be more challenging for cubic functions.
   In some cases, you may be given the roots or the equation is given in factored form otherwise you would need to factor the the cubic equation.
   
3. Plot the Points and Sketch the Graph:
   Plot the intercepts on a coordinate plane.
   Use the end behavior as a guide as to what the “S” like curve will look like.
   

Note:
Calculus is essential for accurately locating critical points and inflection points. Without calculus, you can get a general idea of the shape, but not the precise locations of turning points.

• Show Step-by-step Solutions

How to graph cubic functions using calculus?

• Show Video Lesson

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.