

Solving Equations by Addition or Subtraction
More Lessons for Algebra
Math Worksheets
Let us first look at what is meant by equivalent equations.
Equivalent Equations
An equivalent equation can be obtained from an existing equation in one of four ways.
- Add the same term to both sides of the equation.
- Subtract the same term from both sides.
- Multiply by the same term on both sides.
- Divide by the same term on both sides.
The following four equations are equivalent to x = 5
- Add 3 to both sides: x + 3 = 8
- Subtract 3 from both sides: x – 3 = 2
- Multiply by 3 on both sides: 3x = 15
- Divide by 3 on both sides:
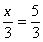
Solving equations
We can use equivalent equations to solve an equation. The solution is obtained when the variable is by itself on one side of the equation. The objective, then, is to use equivalent equations to isolate the variable on one side of the equation.
Consider the equation x + 6 = 14. For it to be considered solved, the x has to be on a side by itself. How can you get rid of the +6 that is also on that side? Remember that a term and its additive inverse add up to 0. The additive inverse of +6 is –6. To write an equivalent equation, subtract 6 from both sides.
Example:
Solve x + 6 = 14
Solution:
x + 6 = 14
x + 6 – 6 = 14 – 6 (Subtract 6 from both sides)
x = 8
Check:
x + 6 = 14
8 + 6 = 14 (Substitute x = 8 into original equation)
To solve the equation y – 4 = 12, we would need to write an equivalent equation with y on a side by itself. To get rid of –4, we would need to add 4 to both sides of the equation.
Example:
Solve y – 4 = 12
Solution:
y – 4 = 12
y – 4 + 4 = 12 + 4 (Add 4 to both sides)
y = 16
Check:
y – 4 = 12
16 – 4 = 12 (Substitute y =16 into original equation)
This video shows students how to solve simple 1-step Algebra equations involving only addition or subtraction.
This video shows students how to solve simple 1-step Algebra equations involving only multiplication or division.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.