Square and Square Root Examples

Understanding squares and square roots is fundamental in mathematics and has applications in various fields like geometry, physics, and engineering.

What are Squares and Square Roots?
The square of a number means to multiply the number by itself. In exponent form, it will have an exponent of 2.
For example, the square of 4 is 4² = 4 × 4 = 16.
The opposite of squaring a number is finding the square root. Since 4² = 16, the square root of 16 is 4.

In this lesson, we will learn about squares and square roots of perfect squares. A perfect square is a whole number that can be obtained by squaring another whole number.

The following diagram shows how to find the square root of some perfect squares. Scroll down the page for more examples and solutions of squares and square roots.

 

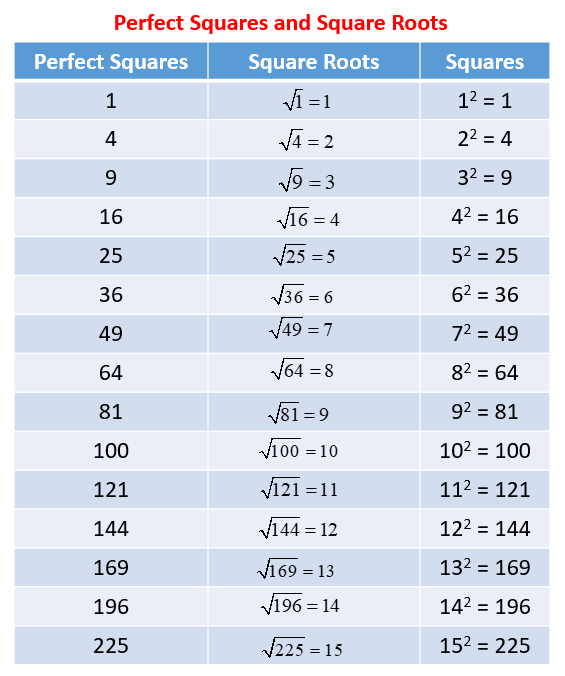
Non-Perfect Squares and Irrational Square Roots:
If a number is not a perfect square, its square root will be an irrational number (a non-repeating, non-terminating decimal).
√2 ≈ 1.41421356…
√7 ≈ 2.64575131…

Exponent Worksheets
Practice your skills with the following exponent worksheets:
Printable & Online Exponent Worksheets

Properties of Perfect Squares

1. Always non-negative (since squaring a real number never gives a negative result).
2. End with specific digits: 0, 1, 4, 5, 6, or 9 (but never 2, 3, 7, or 8).
3. If a number ends with an odd number of zeros, it’s not a perfect square (e.g., 1000 is not a perfect square).

Finding square roots of perfect squares

• Show Video Lesson

Squares and Square Roots

• Show Video Lesson

Square Roots

• Show Video Lesson

Square Roots and Radicals

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.