Squares and Square Roots
Related Topics:
More Lessons for Grade 6
Math Worksheets
Examples, videos, worksheets, and solutions to help students learn about squares, how to simplify square roots and the key properties of square roots.
The square of a number means to multiply the number by itself.
In exponent form, it will have an exponent of 2.
For example, the square of 3 is 32 = 3 × 3 = 9.
The opposite of squaring a number is finding the square root.
Since 32 = 9, the square root of 9 is 3.
The following diagram shows the some of the properties of square roots. Scroll down the page for more examples and solutions of squares and square roots.
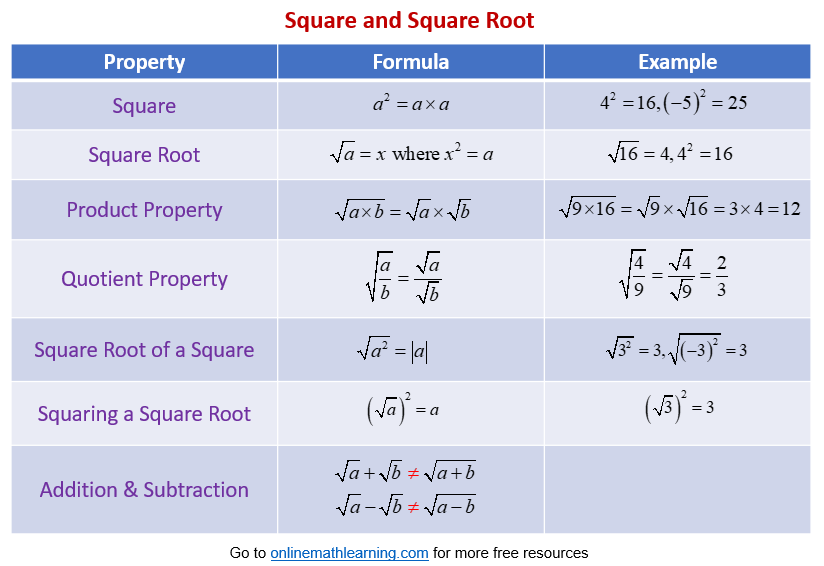
Properties of Square Roots:
- What is a square root?
The square root of a number ‘a’ is a number ‘b’ such that when ‘b’ is multiplied by itself, it equals ‘a’ (i.e., b² = a).
The principal (positive) square root of ‘a’ is denoted by √a. - Product Property:
The square root of a product of two non-negative numbers is equal to the product of their square roots: √(ab) = √a × √b (for a ≥ 0 and b ≥ 0)
Example: √(9 × 4) = √36 = 6, and √9 × √4 = 3 × 2 = 6 - Quotient Property:
The square root of a quotient of a non-negative number and a positive number is equal to the quotient of their square roots: √(a/b) = √a / √b (for a ≥ 0 and b > 0)
Example: √(16/4) = √4 = 2, and √16 / √4 = 4 / 2 = 2 - Square Root of a Square:
The square root of a number squared is the absolute value of that number: √(a²) = |a|
This is because the square root symbol (√) denotes the principal (non-negative) root.
Example: √((-5)²) = √25 = 5 = |-5|, and √(3²) = √9 = 3 = |3| - Squaring a Square Root:
Squaring the principal square root of a non-negative number gives the original number: (√a)² = a (for a ≥ 0)
Example: (√7)² = 7 - Square Roots of Negative Numbers:
The square root of a negative real number is not a real number. It is defined using the imaginary unit ‘i’, where i² = -1.
√(-a) = i√a (for a > 0) - Addition and Subtraction:
Square roots can only be added or subtracted directly if they have the same radicand (the number under the square root symbol): a√c + b√c = (a + b)√c a√c - b√c = (a - b)√c
Square roots with different radicands cannot be simplified by direct addition or subtraction: √a + √b ≠ √(a + b) √a - √b ≠ √(a - b) - Simplifying Square Roots:
To simplify a square root, find the largest perfect square factor of the radicand.
√a = √(k² × m) = √k² × √m = |k|√m
Example: √72 = √(36 × 2) = √36 × √2 = 6√2
These properties are fundamental for working with and simplifying expressions involving square roots. They are used extensively in algebra, geometry, and other areas of mathematics.
This video explains some of the properties of square roots and how to use them to simplify square roots.
Introduction to Squares and Square Roots
This video introduces perfect squares and square roots.
How to simplify square roots when the radicand is a perfect square?
Squares and Square Roots
Square Roots tutorial
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.