Subtracting Rational Expressions

Related Pages
Simplifying Rational Expressions
More Algebra Lessons

A rational expression is a fraction in which either the numerator, or the denominator, or both the numerator and the denominator are algebraic expressions.

Subtracting Rational Expressions with Same Denominators

When the denominators of two algebraic fractions are the same, we can subtract the numerators and then simplify when possible.

Example:
Simplify the following expression:

 

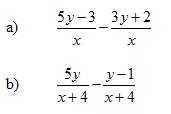
Solution:

 

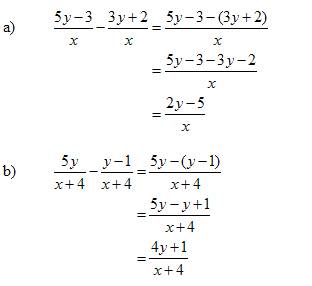
How to subtract rational expressions with same denominators?

Example:
(8f - g)/2 - (8f + g)/2

• Show Video Lesson

How to add and subtract rational expressions with the the same denominators?

Examples:

1. (4x - 1)/(x - 3) + (1 + 3x)/(x - 3) =
2. (x² + 7x)/(x - 7) - (10x + 28)/(x - 7) =

• Show Video Lesson

Subtracting Rational Expressions with Different Denominators

When the denominators of two algebraic fractions are different, we need to find the Least Common Multiple of the denominators (or LCD) before we subtract the fractions.

Here are the steps you need to follow:

Step 1: Find the LCD

Step 2: Express each fraction with the LCD as the denominator.

Step 3: Subtract the numerators and simplify when possible.

Now we apply the above 3 steps in the following example.

Example:
Express the following as a fraction with a single denominator:

 

Solution:

 

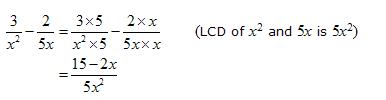
How to subtract rational expressions with different denominators?

Example:
(-7f)/(f - n) - (4f - n)/(4f - 4n) =

• Show Video Lesson

How to subtract rational expressions with different trinomial denominators?

Example:
(3q + 4)/(3q² + 5q - 28) - (5q + 3)/(2q² + 3q - 20)

• Show Video Lesson

How to add and subtract rational expressions when the denominators are different?

Example:
3/(x - 3) + 2/(x + 5)
7/(x + 2) - 5/(x + 3)

• Show Video Lesson

How to subtract rational expressions with unlike denominators?

Example:
(2x + 5)/(x² + 3x -10) - 3/(x + 6)

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.