Illustrative Mathematics Unit 6.1, Lesson 18: Squares and Cubes

Related Topics:
Math Worksheets

Learn how to write and explain the formula for the surface area of a cube. After trying the questions, click on the buttons to view answers and explanations in text or video.

Return to the list of Illustrative Math lessons

Surface Area of a Cube
Let’s write a formula to find the surface area of a cube.

Illustrative Math Unit 6.1, Lesson 18 (printable worksheets)

18.1 - Exponent Review

Select the greater expression of each pair without calculating the value of each expression. Be prepared to explain your choices.

a. 10 · 3 or 10³
b. 13² or 12 · 12
c. 97 + 97 + 97 + 97 + 97 + 97 or 5 · 97

• Answers

  a. 10³.
  10³ is 10 · 10 · 10, which is greater than 10 · 3.

  b. 13².
  13² is 13 · 13, which is greater than 12 · 12.

  c. 97 + 97 + 97 + 97 + 97 + 97.
  This expression is equal to 6 · 97, which is greater than 5 · 97.

• See Video 1 for Whole Lesson
• See Video 2 for Whole Lesson

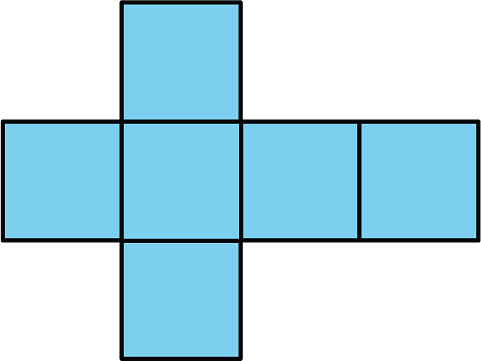
18.2 - The Net of a Cube

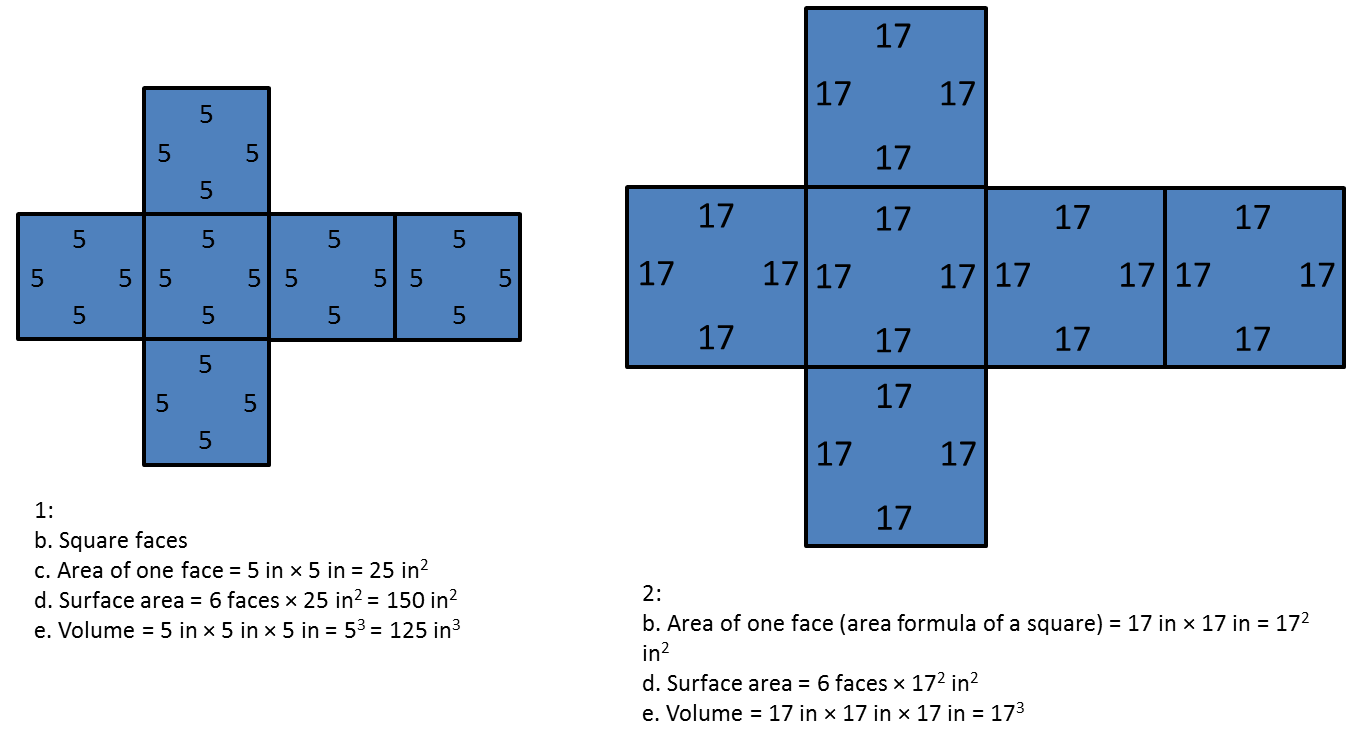
1. A cube has edge length 5 inches.

1. Draw a net for this cube, and label its sides with measurements.
2. What is the shape of each face?
3. What is the area of each face?
4. What is the surface area of this cube?
5. What is the volume of this cube?

2. A cube has edge length 17 units.

1. Draw a net for this cube, and label its sides with measurements.
2. Explain why the area of each face of this cube is 17² square units.
3. Write an expression for the surface area, in square units.
4. Write an expression for the volume, in cubic units.

• See Possible Answers

  

  1. b. Square faces
  c. Area of one face = 5 in × 5 in = 25 in²
  d. Surface area = 6 faces × 25 in² = 150 in²
  e. Volume = 5 in × 5 in × 5 in = 5³ = 125 in³

  2. b. Area of one face (area formula of a square) = 17 in × 17 in = 17² in²
  c. Surface area = 6 faces × 17² in²
  d. Volume = 17 in × 17 in × 17 in = 17³

18.3 - Every Cube in the Whole World

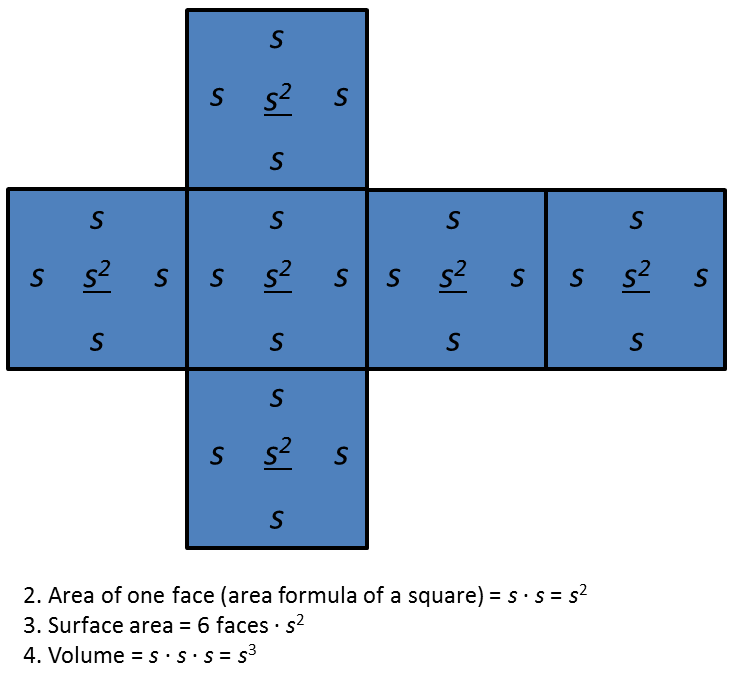
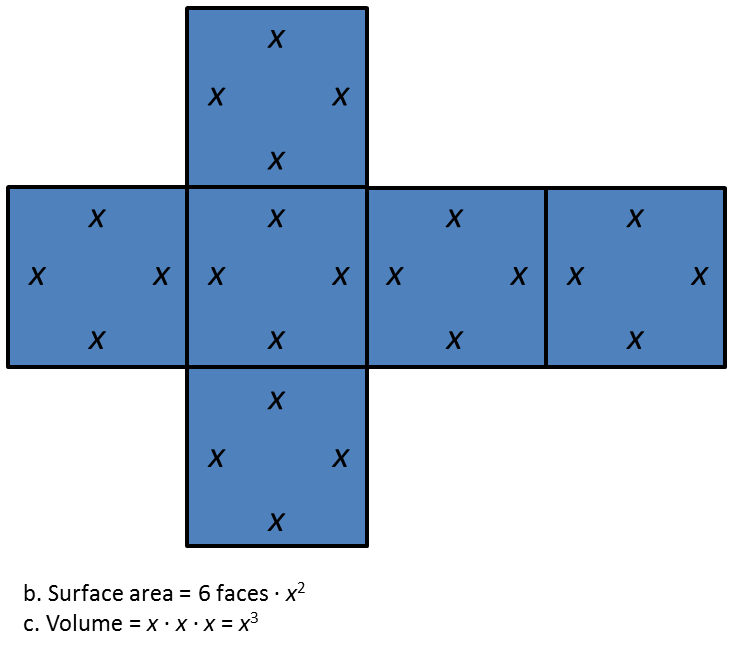
A cube has edge length s.

1. Draw a net for the cube.

2. Write an expression for the area of each face. Label each face with its area.

3. Write an expression for the surface area.

4. Write an expression for the volume.

• See Possible Answers

  

  2. Area of one face (area formula of a square) = s · s = s²
  The area of each face is underlined.

  3. Surface area = 6 faces · s²

  4. Volume = s · s · s = s³

Lesson 18 Summary

• Show Image
  

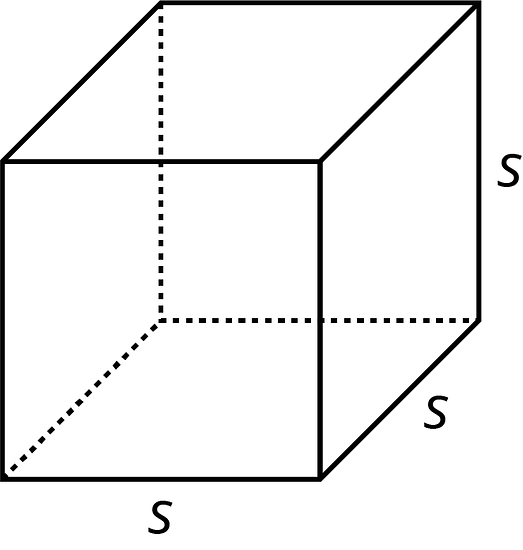
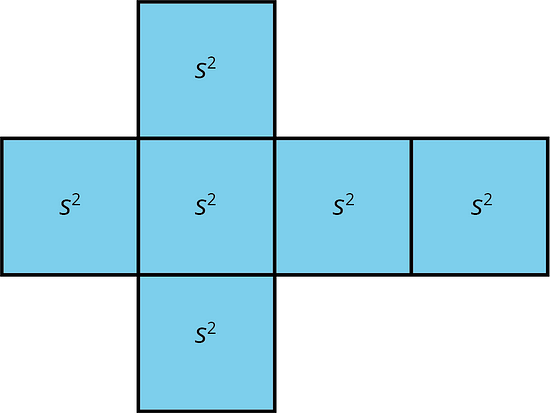
The volume of a cube with edge length s is s³.

A cube has 6 faces that are all identical squares. The surface area of a cube with edge length s is 6 · s².

• Show Image
  

Practice Problems

1. a. What is the volume of a cube with edge length 8 in?
b. What is the volume of a cube with edge length ⅓ cm?
c. A cube has a volume of 8 ft³. What is its edge length?

• Answers

  a. 8³ in³ = 512 in³

  b. (⅓)³ cm³ = ¹⁄₂₇ cm³

  c. 2³ ft³ = 8 ft³
  2 ft is the edge length.

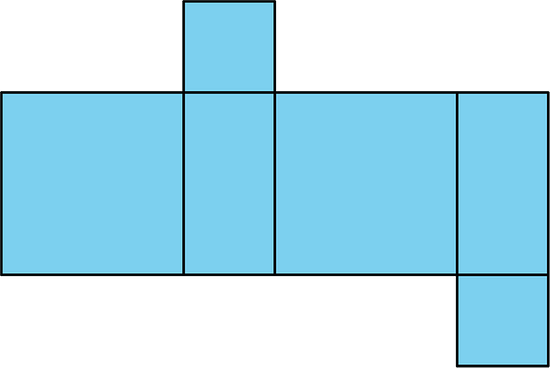
2. a. What three-dimensional figure can be assembled from this net?

• Show Image
  

b. If each square has a side length of 61 cm, write an expression for the surface area and another for the volume of the figure.

• Answers

  a. This net can be assembled into a cube.

  b. Surface area = 6(61²) cm²
  Volume = 61³ cm³

3. a. Draw a net for a cube with edge length x cm.
b. What is the surface area of this cube?
c. What is the volume of this cube?

• Answers

  a.
  

  b. Surface area = 6 faces · x²

  c. Volume = x · x · x = x³

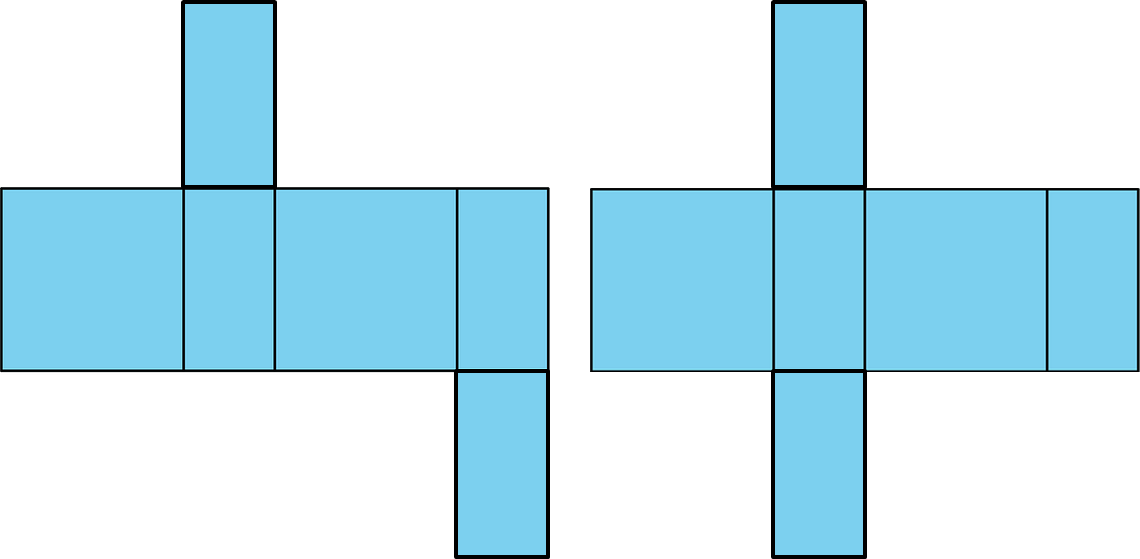
4. Here is a net for a rectangular prism that was not drawn accurately.

• Show Image
  

a. Explain what is wrong with the net.
b. Draw a net that can be assembled into a rectangular prism.
c. Create another net for the same prism.

• See Possible Answers

  a. The square faces are too small to match the entire edge of the large rectangles when the net is folded.

  b and c.
  

5. State whether each figure is a polyhedron. Explain how you know.

• Show Image
  

• Answers

  A is not a polyhedron, while B is a polyhedron. A is a cylinder, which has non-polygonal faces. B is a heptagonal prism and all its faces are polygons.

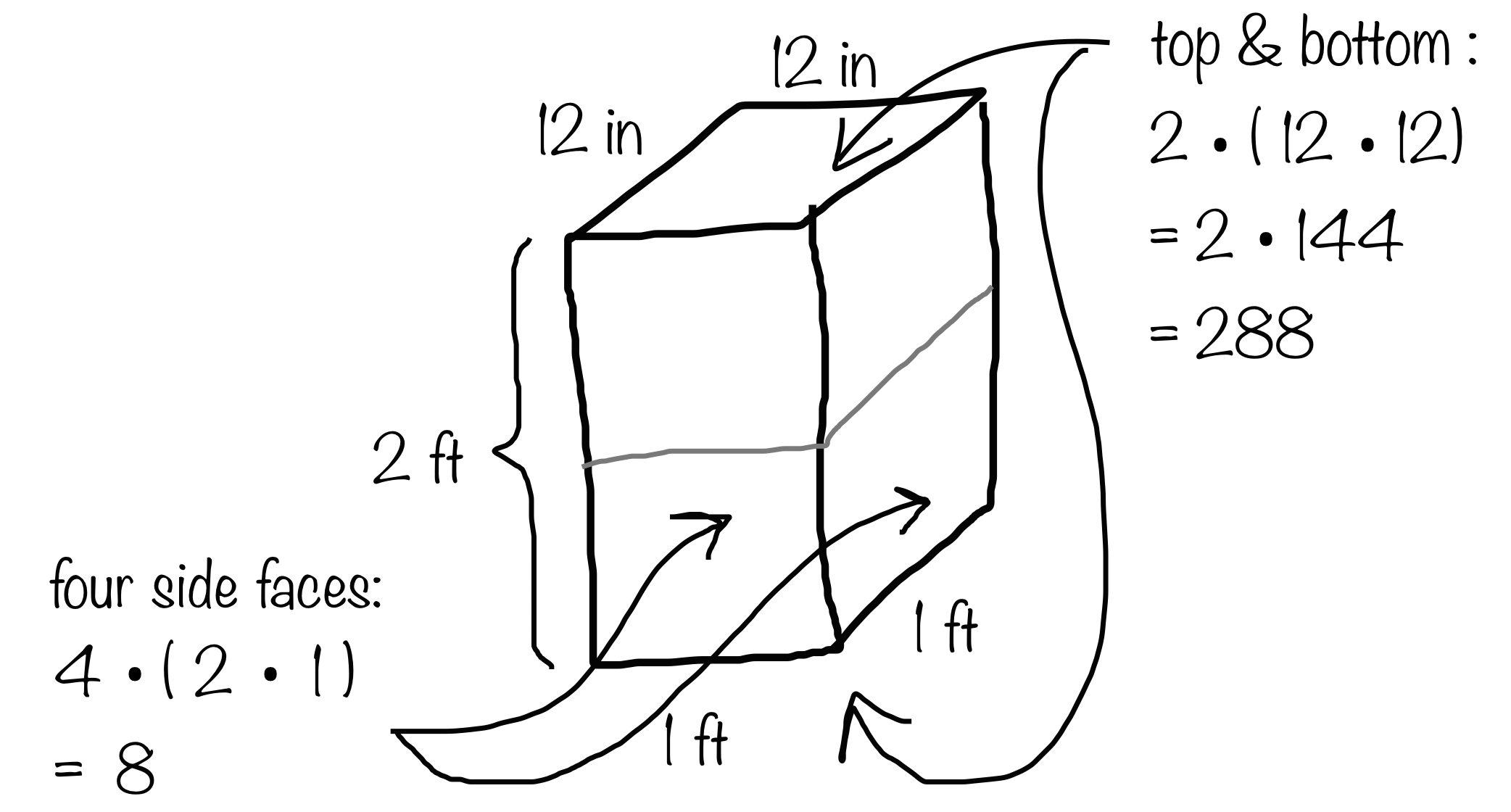
6. Here is Elena’s work for finding the surface area of a rectangular prism that is 1 foot by 1 foot by 2 feet.

• Show Image
  

She concluded that the surface area of the prism is 296 square feet. Do you agree with her conclusion? Explain your reasoning.

• Answers

  Elena is incorrect. The dimensions of the top face have been labeled in inches, which is a different unit from the rest of the labels. Values calculated in square inches (the total area of the top and bottom faces in Elena's sketch and calculations = 288 in²) cannot be added to values calculated in square feet (the total area of the 4 side faces in Elena's sketch and calculations = 8 ft²).

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.