Triangle Sum Worksheets

There are five sets of triangle worksheets:

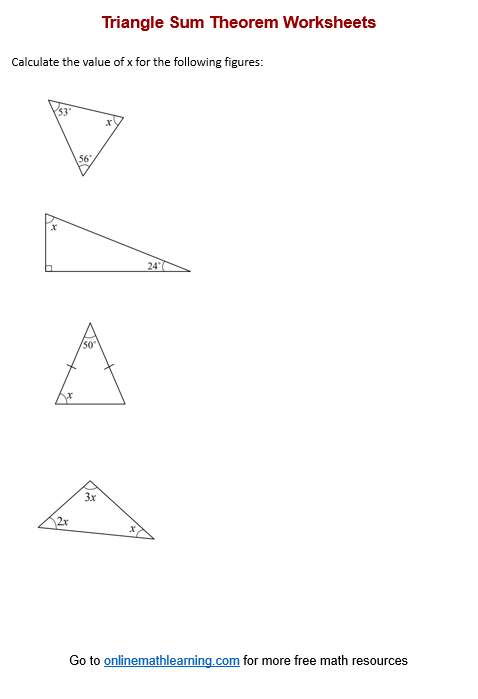
• Triangle Sum Theorem
  
• Exterior Angle Theorem
  
• Area of Triangle
  
• Area of Triangle using Sine
  
• Pythagorean Theorem
  

Examples, solutions, videos, and worksheets to help grade 7 students learn how to find unknown angles using the Triangle Sum Theorem.

How to use the Triangle Sum Theorem?

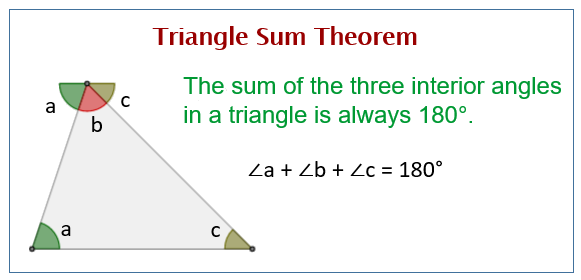
The Triangle Sum Theorem, also known as the Angle Sum Theorem for a triangle, states that the sum of the three interior angles of any triangle is always equal to 180 degrees.

This property is true for all types of triangles, including equilateral triangles (all sides and angles are equal), isosceles triangles (two sides and two angles are equal), and scalene triangles (no sides or angles are equal).

Mathematically, if you have a triangle with three interior angles ∠A, ∠B, and ∠C, the triangle sum theorem can be expressed as:

∠A + ∠B + ∠C = 180 degrees

This property is widely used in geometry to solve for unknown angles within triangles or to prove various theorems and relationships involving angles in triangles.

For example, if you know two of the interior angles of a triangle, you can find the measure of the third angle by subtracting the sum of the known angles from 180 degrees:

∠C = 180 degrees - (∠A + ∠B)

Understanding the triangle sum theorem is essential for working with triangles and solving problems related to angles in geometric figures.

 

Have a look at this video if you need to review how to find unknown angles using the Triangle Sum Theorem.

• Triangle Sum Theorem

Click on the following worksheet to get a printable pdf document.
Scroll down the page for more Triangle Sum Worksheets.

 

More Triangle Sum Worksheets

Printable
(Answers on the second page.)
Triangle Sum Worksheet

Online
Angles in a Triangle 1
Angles in a Triangle 2

Quadrilateral Properties
Angles in a Quadrilateral

Angles in Polygons
Interior Angles in Polygons
Exterior Angles in Polygons

Related Lessons & Worksheets

Triangle Sum Theorem

More Printable Worksheets

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.