Illustrative Mathematics Unit 6.6, Lesson 17: Two Related Quantities, Part 2

Related Pages
Illustrative Math
Grade 6

Lesson 17: Two Related Quantities, Part 2

Let’s use equations and graphs to describe stories with constant speed.

Illustrative Math Unit 6.6, Lesson 17 (printable worksheets)

Lesson 17 Summary

In this lesson, we will learn how to use equations and graphs to describe stories with constant speed.
The following diagram shows how to use equations to describe problems with constant speeds.

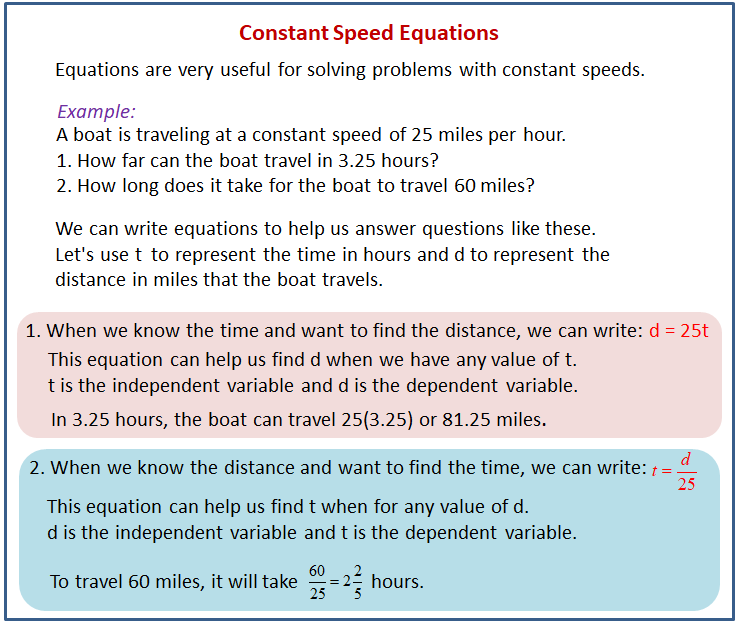
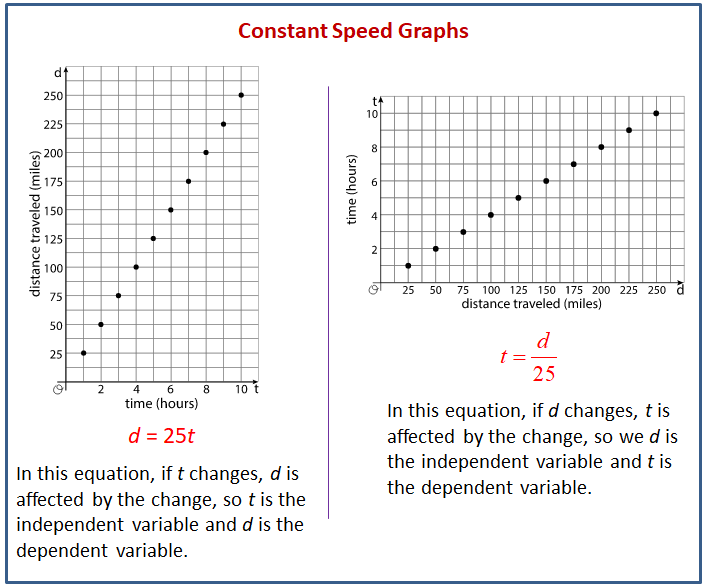
The following diagram shows how to use graphs to describe problems with constant speeds.

Lesson 17.1 Walking to the Library

Lin and Jada each walk at a steady rate from school to the library. Lin can walk 13 miles in 5 hours, and Jada can walk 25 miles in 10 hours. They each leave school at 3:00 and walk 3¼ miles to the library. What time do they each arrive?

• See Video for Whole Lesson

Scroll down the page for the solutions to the “Are you ready for more?” section.

Lesson 17.2 The Walk-a-thon

Diego, Elena, and Andre participated in a walk-a-thon to raise money for cancer research. They each walked at a constant rate, but their rates were different.

1. Complete the table to show how far each participant walked during the walk-a-thon
   

time in hours	miles walked by Diego	miles walked by Elena	miles walked by Andre
1
2	6
	12	11
5			17.5

2. How fast was each participant walking in miles per hour?
3. How long did it take each participant to walk one mile?
4. Graph the progress of each person in the coordinate plane. Use a different color for each participant.

[See Applet](https://access.openupresources.org/curricula/our6-8math/en/supporting-material/7515/index.html)

5. Diego says that d = 3t represents his walk, where d is the distance walked in miles and t is the time in hours.
a. Explain why d = 3t relates the distance Diego walked to the time it took.
b. Write two equations that relate distance and time: one for Elena and one for Andre.
6. Use the equations you wrote to predict how far each participant would walk, at their same rate, in 8 hours.
7. For Diego’s equation and the equations you wrote, which is the dependent variable and which is the independent variable?

Are you ready for more?

1. Two trains are traveling toward each other, on parallel tracks. Train A is moving at a constant speed of 70 miles per hour. Train B is moving at a constant speed of 50 miles per hour. The trains are initially 320 miles apart. How long will it take them to meet?
   
2. How long will it take a train traveling at 120 miles per hour to go 320 miles?
3. Explain the connection between these two problems.
   
   • Show Answer

     

Lesson 17 Practice Problems

1. A car is traveling down a road at a constant speed of 50 miles per hour.
   a. Complete the table with the amounts of time it takes the car to travel certain distances, or the distances traveled for certain amounts of time.
   

time (hours)	distance (miles)
2
1.5
t
	50
2	300
2	d

b. Write an equation that represents the distance traveled by the car, d, for an amount of time, t.
c. In your equation, which is the dependent variable and which is the independent variable?
2. The graph represents the amount of time in hours it takes a ship to travel various distances in miles.
a. Write the coordinates of one of point on the graph. What does the point represent?
b. What is the speed of the ship in miles per hour?
c. Write an equation that relates the time, t, it takes to travel a given distance, d.
3. Find a solution to each equation in the list that follows (not all numbers will be used):
4. Select all the expressions that are equivalent to 5x + 30 - 15x.
A. 5(x + 6x - 3x)
B. (5 + 30 - 15) · x
C. x(5 + 3x - 15x)
D. 5x(1 + 6 - 3)
E. 5(x + 30x - 15x)

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.