Volume Of A Pyramid
In these lessons, we will learn
- what is a pyramid?
- how to find the volume of a pyramid with rectangular or square bases.
- how to find the volume of a pyramid with different types of bases.
- how to solve word problems about pyramids.
- how to demonstrate the relationship between the volume of a pyramid and the volume of a prism with the same base and height.
Related Pages
Volume Formulas
Volume Of Cylinders
Explanations For The Surface Area Formulas
More Geometry Lessons
Solid geometry is concerned with three-dimensional shapes.
Pyramids
A pyramid is a solid with a polygon base and connected by triangular faces to its vertex. The lateral faces meet at a common vertex. The height of the pyramid is the perpendicular distance from the base to the vertex.
A pyramid is a regular pyramid if its base is a regular polygon and the triangular faces are all congruent isosceles triangles. The pyramid is named after the shape of its base. A rectangular pyramid has a rectangle base. A triangular pyramid has a triangle base.
A right pyramid is a pyramid in which the vertex is vertically above the center of the base. If the vertex is not vertically above the center of the base then it is an oblique pyramid.
Volume Of Pyramids
The volume of a pyramid is equal to one-third the product of the area of the base and the height.
The volume of a pyramid is given by the formula:
Worksheet: calculate the volumes of square pyramids
Worksheet: calculate the volumes of prisms & pyramids
Example:
Find the volume of a pyramid with a rectangular base measuring 6 cm by 4 cm and height 10 cm.
Solution:
Volume
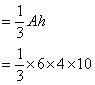
= 80 cm3
Example:
The following figure is a right pyramid with an isosceles triangle base. Find the volume of the pyramid
if the height is 20 cm.
Solution:
First, we have to calculate the area of the base.
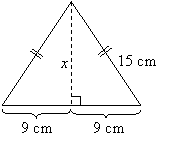
To do that, we would need to get the height of the isosceles triangle that forms the base.
Using Pythagorean theorem,
Area of triangle
= 
= 108 cm2
Volume of pyramid
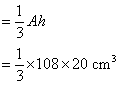
= 720 cm3
Volume of a Pyramid with Rectangular or Square Base
This video gives the formula to find the volume of a pyramid and uses it to find the volume of a pyramid with a rectangular base.
How to find the volume of a pyramid?
Example:
Find the volume of a pyramid given s = 9ft, h = 5ft, l = 8ft.
How to calculate the volume of a pyramid?
Example:
The base of the following pyramid is a square. What is the volume of the pyramid?
Volume of a pyramid: Calculate height using Pythagorean Theorem
Volume Of Pyramid With Different Types Of Bases
Volume Of A Triangular And Square Pyramid
How to find the volume of a square pyramid and a triangular pyramid and compare how they are the same and how they are different?
Volume of a Hexagonal Pyramid
Example:
Find the volume of a hexagonal pyramid that has a height of 8 and a base edge of 10.
Word Problems About The Volume Of Pyramids
Find the height of a pyramid given the volume and base dimensions.
Example:
The base of the following pyramid is a square. If the volume of the pyramid is 360 ft3,
what is the missing length?
Example:
The volume of a pyramid is 80cm3, base is a triangle, find the height.
Volume of a Pentagonal Pyramid
Example:
Find the surface area of a regular pentagonal pyramid given an altitude of 4 and a slant height of 5.
Given the altitude and slant height we can find the apothem.
Using the apothem, we can find the area of the base.
The volume of the pyramid is 1/3 the area of the base multiply by the height.
Examples:
- A square pyramid has a height of 7 m and a base that measures 2 m on each side. Find the volume of the pyramid. Explain whether doubling the height would double the volume of the pyramid.
- The volume of a prism is 27 in3. What is the volume of a pyramid with the same base and height?
Demonstrate the formula of the volume of a pyramid
This video will demonstrate that the volume of a pyramid is one-third that of a prism with the same base and height and that the volume of a cone is on-third that of a cylinder with the same base and height. This is not a formal proof.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.