Volume of Prisms: Examples
Examples, videos, worksheets, and solutions to help Grade 8 students learn how to find the volume of different types of prisms.
How to find the volume of a prism?
To find the volume of a prism, you need to know two things:
- The area of the base (B): The base of a prism can be any polygon (triangle, square, rectangle, pentagon, hexagon, etc.). You’ll need to use the appropriate formula to calculate the area of that specific polygon.
- The height of the prism (h): The height is the perpendicular distance between the two bases of the prism.
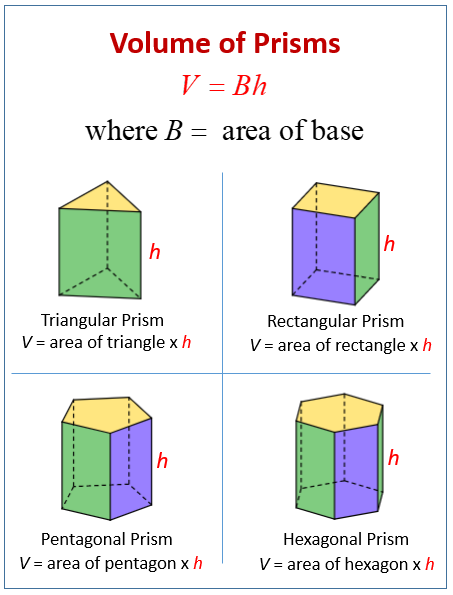
The formula for the volume of any prism is:
Volume (V) = Area of the base (B) × Height (h)
Multiply the area of the base by the height to get the volume.
The following diagram gives the volume of prism formula. Scroll down the page for more examples and solutions on how to use the volume of prism formula.
Geometry Worksheets
Practice your skills with the following Geometry Worksheets:
Printable & Online Geometry Worksheets
How to apply the formula to different types of prisms:
- Rectangular Prism (including cubes):
Base: Rectangle
Area of the base (B): length (l) × width (w)
Volume (V): l × w × h - Triangular Prism:
Base: Triangle
Area of the base (B): \(\frac{1}{2}\) × base of triangle (b) × height of triangle (h_triangle)
Volume (V): (\(\frac{1}{2}\) × b × h_triangle) × h_prism - Cylinder:
While technically not a prism (it has circular bases and a curved side), it follows the same volume principle:
Base: Circle
Area of the base (B): π × radius² (πr²)
Volume (V): πr² × h - Trapezoidal Prism:
Base: Trapezoid
Area of the base (B): \(\frac{1}{2}\) × (base1 + base2) × height of trapezoid (h_trapezoid)
Volume (V): [\(\frac{1}{2}\) × (base1 + base2) × h_trapezoid] × h_prism - Pentagonal Prism:
Base: Pentagon
The area of a regular pentagon is given by: \(\left(\frac{5}{2}\right)\) × side length × apothem
Volume (V): Area of the pentagonal base × h_prism - Hexagonal Prism:
Base: Hexagon
The area of a regular hexagon is given by: \(\left(\frac{3\sqrt{3}}{2}\right)\) × side length²
Volume (V): Area of the hexagonal base × h_prism
Volume of Prisms
Math lesson demonstrating how to find the volume of rectangular and triangular Prisms.
- Find the area of the base.
- Multiply the area of the base by the height.
Volume of rectangular prism, triangular prism and trapezoidal prism
Volumes of Prisms
Specifically the volume of a Rectangular-Based Prism and a Cylinder in simplest pi form.
Calculating the volume of oblique prisms and cylinders
Does the volume of stack of CDs or pennies change if the stack is skewed? No
Use Cavalieri’s Principle to find the volume of the oblique cylinder.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.