How To Prove Triangles Congruent - SSS, SAS, ASA, AAS Rules

Congruent Triangles

Congruent Triangles
Rules for Triangle Congruency	SSS Rule	SAS Rule
ASA Rule	AAS Rule	Two-column Proofs

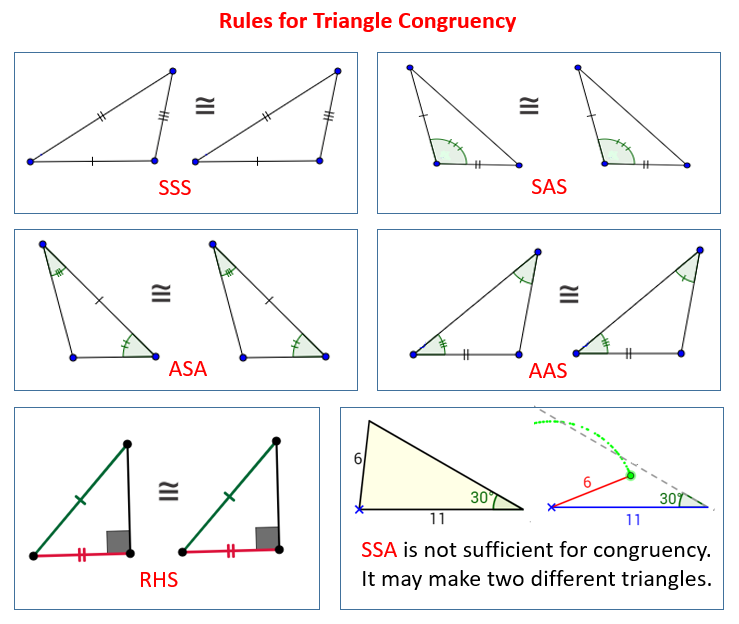
Rules for Triangle Congruency

Congruent triangles are triangles that have the same size and shape. This means that the corresponding sides are equal and the corresponding angles are equal.

We can tell whether two triangles are congruent without testing all the sides and all the angles of the two triangles. In this lesson, we will consider the four rules to prove triangle congruence. They are called the SSS rule, SAS rule, ASA rule and AAS rule.
In another lesson, we will consider a proof used for right triangles called the Hypotenuse Leg rule. As long as one of the rules is true, it is sufficient to prove that the two triangles are congruent.

The following diagrams show the Rules for Triangle Congruency: SSS, SAS, ASA, AAS and RHS. Take note that SSA is not sufficient for Triangle Congruency. Scroll down the page for more examples, solutions and proofs.

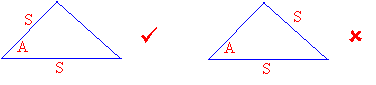
Side-Side-Side (SSS) Rule

Side-Side-Side is a rule used to prove whether a given set of triangles are congruent.

The SSS rule states that:
If three sides of one triangle are equal to three sides of another triangle, then the triangles are congruent.

In the diagrams below, if AB = RP, BC = PQ and CA = QR, then triangle ABC is congruent to triangle RPQ.

Side-Angle-Side (SAS) Rule

Side-Angle-Side is a rule used to prove whether a given set of triangles are congruent.

The SAS rule states that:
If two sides and the included angle of one triangle are equal to two sides and included angle of another triangle, then the triangles are congruent.

An included angle is an angle formed by two given sides.

Included Angle           Non-included angle

For the two triangles below, if AC = PQ, BC = PR and angle C< = angle P, then by the SAS rule, triangle ABC is congruent to triangle QRP.

Angle-Side-Angle (ASA) Rule

Angle-side-angle is a rule used to prove whether a given set of triangles are congruent.

The ASA rule states that:
If two angles and the included side of one triangle are equal to two angles and included side of another triangle, then the triangles are congruent.

Angle-Angle-Side (AAS) Rule

Angle-side-angle is a rule used to prove whether a given set of triangles are congruent.

The AAS rule states that:
If two angles and a non-included side of one triangle are equal to two angles and a non-included side of another triangle, then the triangles are congruent.

In the diagrams below, if AC = QP, angle A = angle Q, and angle B = angle R, then triangle ABC is congruent to triangle QRP.

Three Ways To Prove Triangles Congruent

A video lesson on SAS, ASA and SSS.

1. SSS Postulate: If there exists a correspondence between the vertices of two triangles such that three sides of one triangle are congruent to the corresponding sides of the other triangle, the two triangles are congruent.
2. SAS Postulate: If there exists a correspondence between the vertices of two triangles such that the two sides and the included angle of one triangle are congruent to the corresponding parts of the other triangle, the two triangles are congruent.
3. ASA Postulate: If there exits a correspondence between the vertices of two triangles such that two angles and the included side of one triangle are congruent to the corresponding parts of the other triangle, the two triangles are congruent.

• Show Video Lesson

Using Two Column Proofs To Prove Triangles Congruent

Triangle Congruence by SSS
How to Prove Triangles Congruent using the Side Side Side Postulate?
If three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent.

• Show Video Lesson

Triangle Congruence by SAS
How to Prove Triangles Congruent using the SAS Postulate?
If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent.

• Show Video Lesson

Prove Triangle Congruence with ASA Postulate
How to Prove Triangles Congruent using the Angle Side Angle Postulate?
If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.

• Show Video Lesson

Prove Triangle Congruence by AAS Postulate
How to Prove Triangles Congruent using the Angle Angle Side Postulate?
If two angles and a non-included side of one triangle are congruent to two angles and a non-included side of another triangle, then the two triangles are congruent.

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.